以下是针对您提供的滚动轴承动力学模型程序(包括刚性保持架模型和柔性保持架模型)的技术分析文章。文章严格围绕代码结构、功能模块、建模方法与输出结果展开,参考文献仅作背景支持,不涉及外部文献内容。
—
# 滚动轴承动力学建模与仿真分析:刚性/柔性保持架模型对比
## 一、概述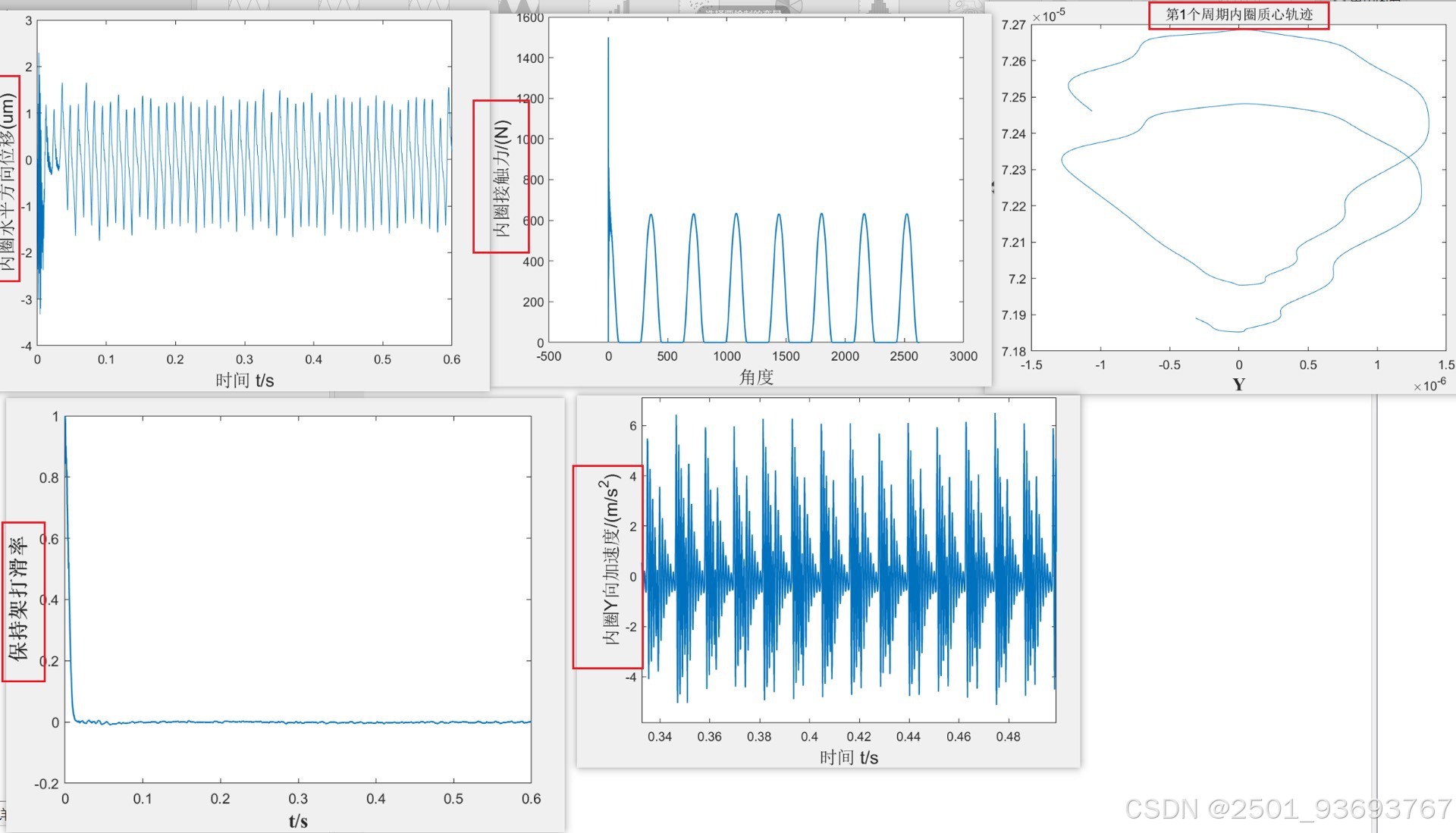
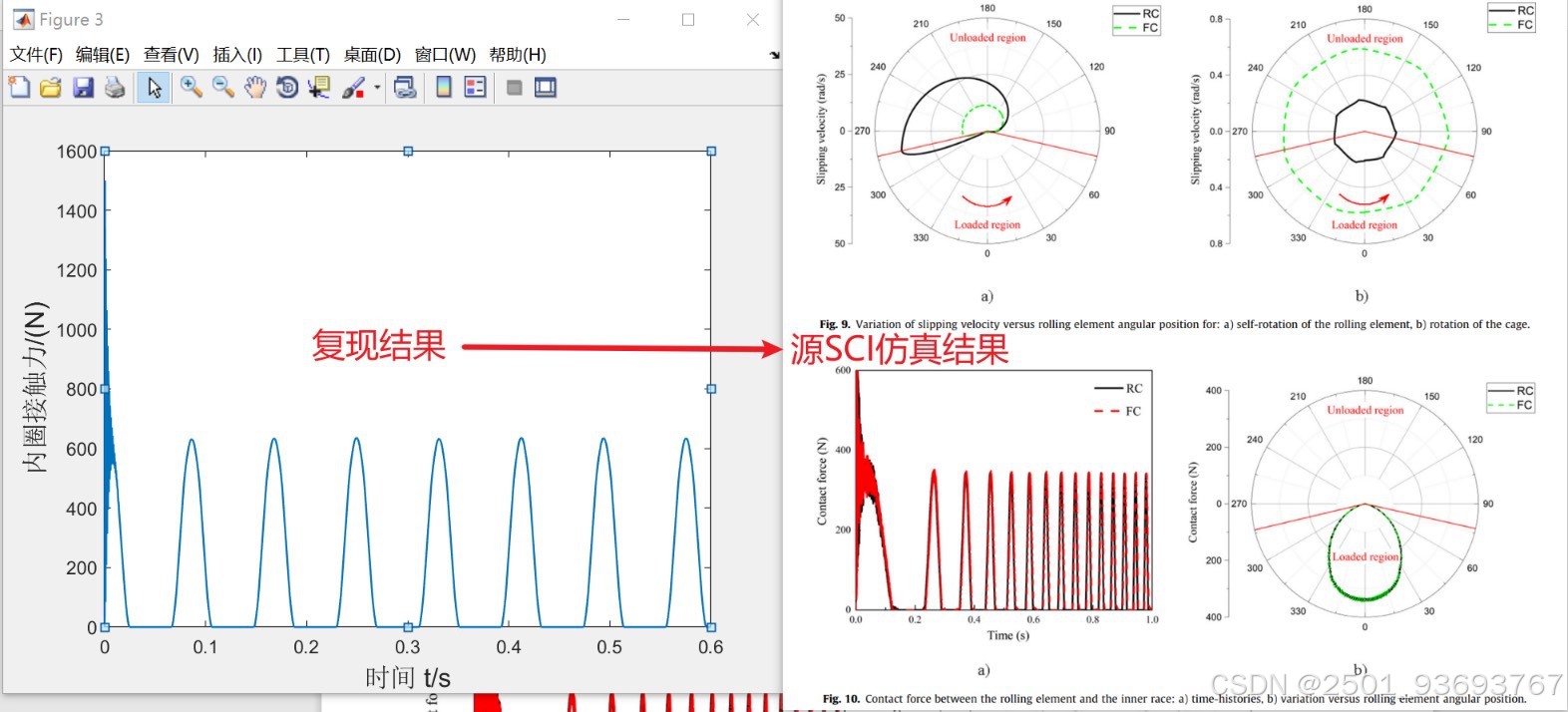
本文基于MATLAB环境下的滚动轴承动力学仿真程序,对两种保持架模型——**刚性保持架模型**与**柔性保持架模型**——进行了建模与仿真分析。程序通过四阶龙格-库塔法(RK-4)求解多体动力学方程,综合考虑了滚动体与内外圈的接触力、摩擦力、阻尼效应、离心力等因素,并输出了包括内圈轨迹、保持架转速、打滑率、接触力等在内的多项动力学响应。
## 二、程序结构概述
### 1. 核心求解器:`RK_4.m`
两个模型均采用相同的四阶龙格-库塔数值积分方法,用于求解常微分方程组。该函数支持变步长积分,适用于高维非线性动力学系统。
“`matlab
function [t,y] = RK_4(f, t0, tN, y0, h)
“`
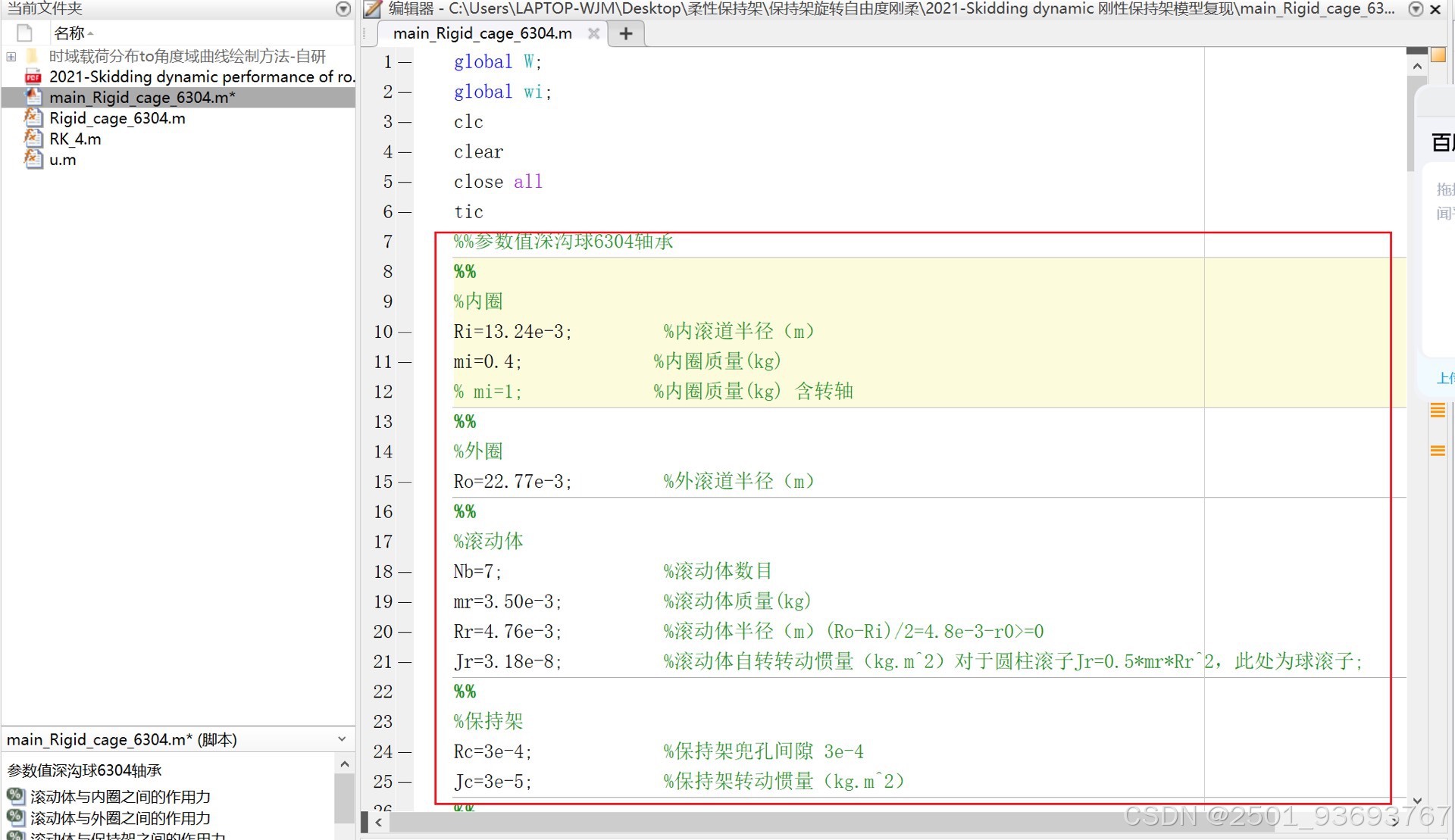
### 2. 刚性保持架模型
– **主函数**:`Rigid_cage_6304.m`
– **主程序**:`main_Rigid_cage_6304.m`
#### 建模特点:
– 保持架视为刚性体,无变形;
– 考虑滚动体与保持架兜孔的碰撞;
– 考虑滚动体与内外圈的Hertz接触;
– 考虑滑动摩擦与离心力;
– 系统阻尼设为300 N·s/m。
#### 状态变量:
– 内圈位移与速度;
– 保持架转角与角速度;
– 滚动体径向位移、公转角、自转角及其速度。
#### 输出图形包括:
– 保持架转速;
– 滚动体与保持架碰撞力;
– 内圈接触力(时域与角度域);
– 内圈加速度;
– 保持架与滚动体打滑率;
– 滚动体运动状态(公转、自转、径向加速度);
– 内圈质心轨迹。
### 3. 柔性保持架模型
– **主函数**:`flex_cage_6304.m`
– **主程序**:`main_flex_cage_6304.m`
#### 建模特点:
– 保持架被离散为多个质量块,通过弹簧-阻尼单元连接;
– 引入保持架相邻单元之间的相互作用力 `Ncc`;
– 可模拟保持架的整体变形与局部弹性;
– 其余物理模型与刚性模型一致。
#### 新增状态变量:
– 每个保持架离散单元的转角与角速度;
– 相邻单元之间的相对位移与弹簧力。
#### 新增输出:
– 保持架相邻单元间的弹簧作用力;
– 单个保持架离散单元的运动响应。
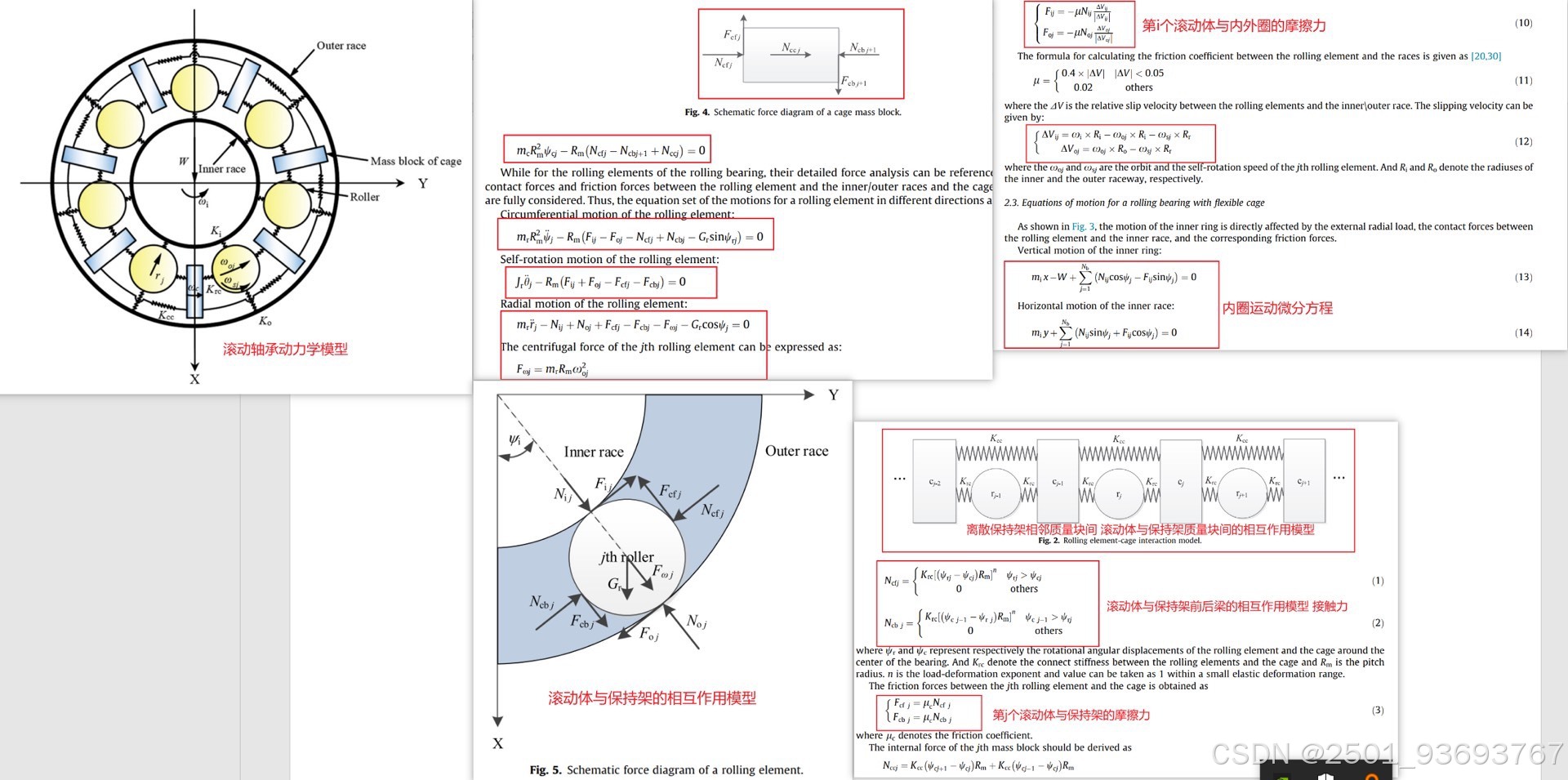
## 三、关键物理模型与代码实现
### 1. 接触力模型
滚动体与内外圈的接触力采用Hertz接触理论:
“`matlab
if deltai(j) <= 0
Ni(j) = 0;
else
Ni(j) = Ki * (deltai(j))^n;
end
“`
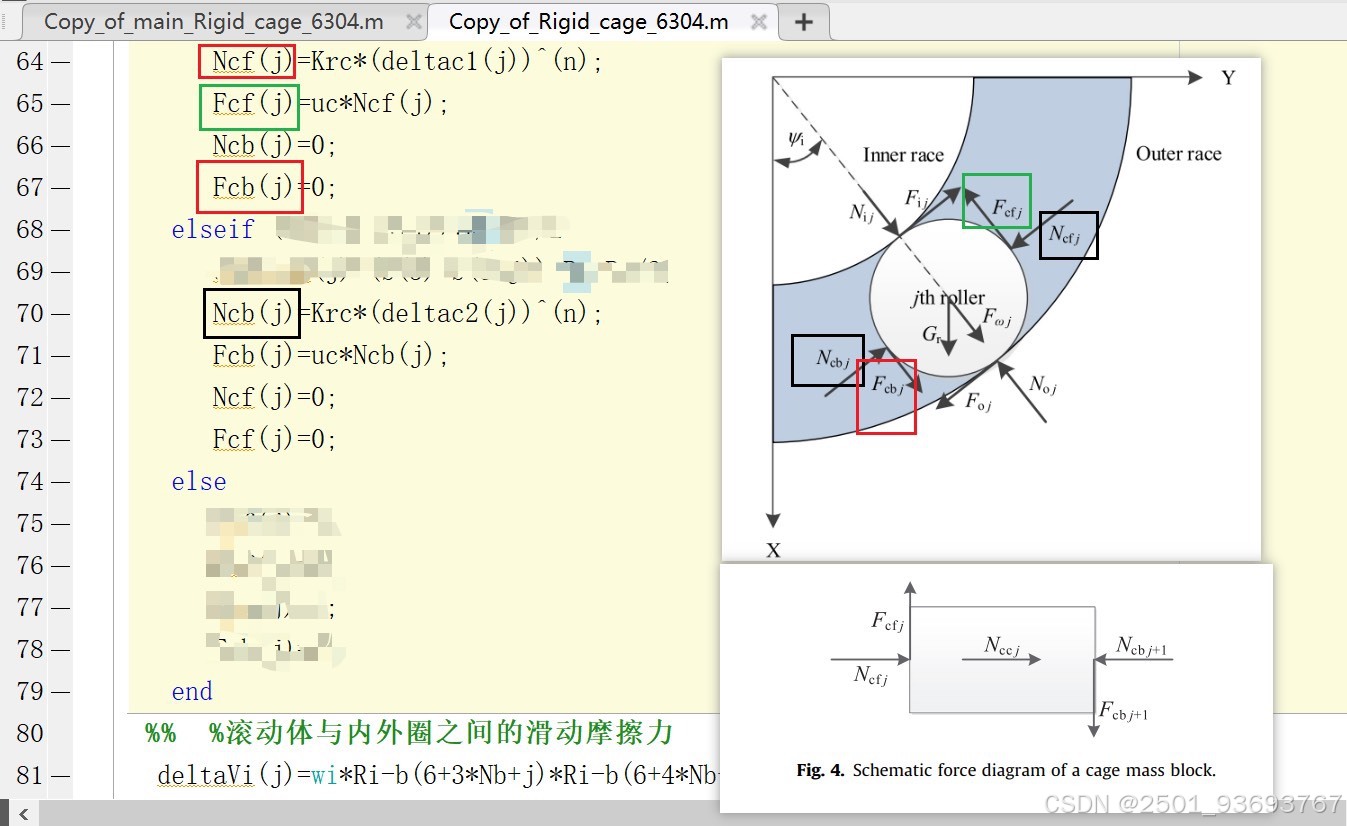
### 2. 保持架与滚动体碰撞模型
判断滚动体是否与保持架兜孔发生碰撞:
“`matlab
if (b(3+Nb+j) – b(3)) * Rm > Rc/2
% 正向碰撞
elseif (b(3) – b(3+Nb+j)) * Rm > Rc/2
% 反向碰撞
else
% 无碰撞
end
“`
### 3. 摩擦力模型
采用非线性摩擦系数函数 `u.m`,考虑速度对摩擦系数的影响:
“`matlab
function u = u(deltaV)
A = -7.5e-3;
B = 1.99e-2;
C = 1.6;
D = 7.5e-3;
if deltaV == 0
u = 0;
else
u = ((A + B.*abs(deltaV)) * exp(-C*abs(deltaV)) + D) * (deltaV/abs(deltaV));
end
end
“`
### 4. 柔性保持架弹簧力模型
相邻保持架单元之间的弹簧力:
“`matlab
dcc(j) = (b(4+j) – b(3+j)) * Rm + (b(2+j) – b(3+j)) * Rm;
Ncc(j) = Kcc * dcc(j);
“`
## 四、仿真输出与分析
### 1. 时域响应
– **保持架转速**:反映其运动稳定性;
– **内圈接触力**:显示载荷分布随时间变化;
– **碰撞力**:评估保持架与滚动体之间的冲击强度;
– **打滑率**:衡量运动传递效率。
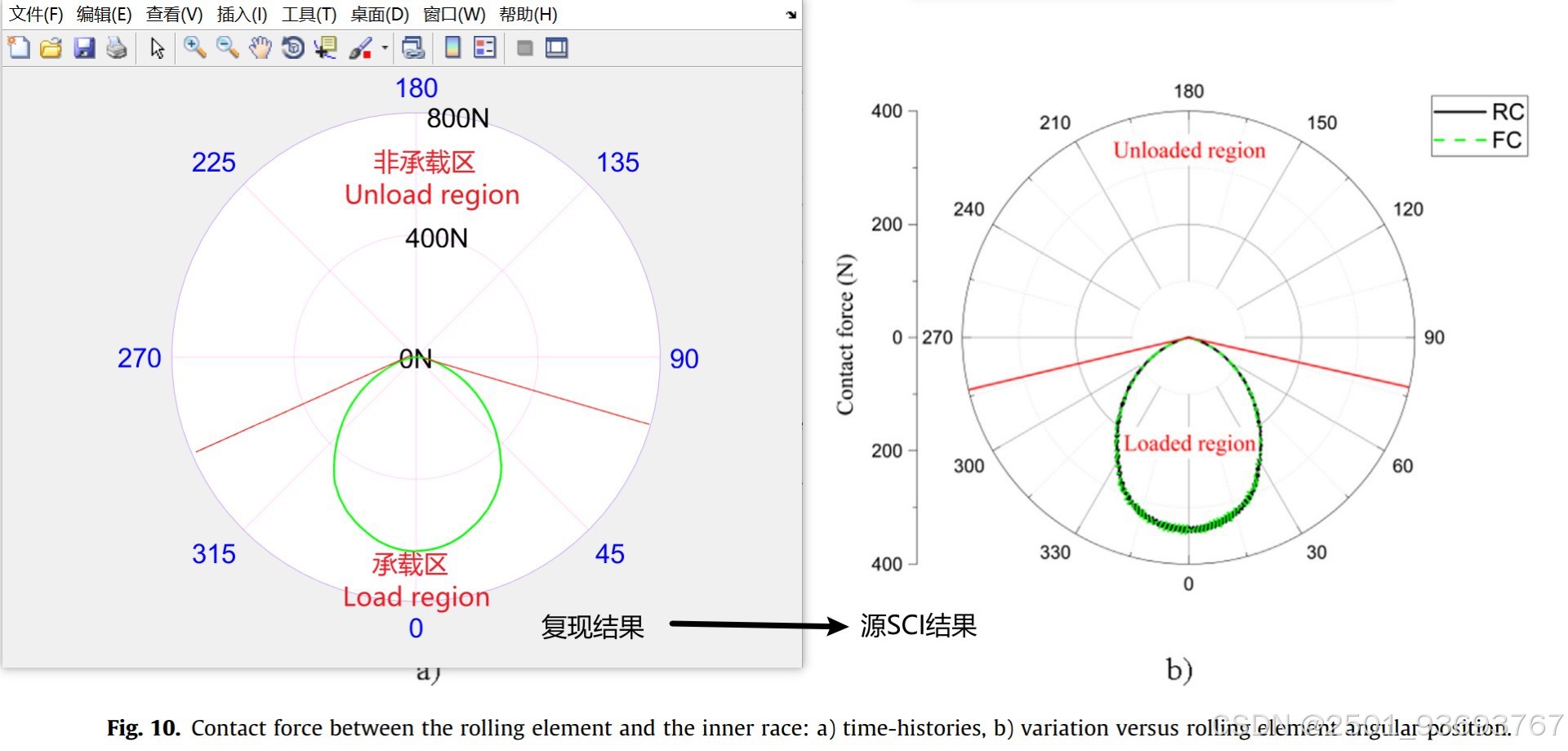
### 2. 角度域响应
– 将时间域接触力转换为角度域分布,便于分析周期性载荷;
– 使用 `polarplot` 绘制极坐标下的接触力分布。
### 3. 轨迹与运动状态
– **内圈质心轨迹**:反映内圈在径向平面内的运动路径;
– **滚动体运动状态**:包括公转、自转角速度与径向加速度。
## 五、结论
本文基于MATLAB代码实现了滚动轴承的刚性保持架与柔性保持架动力学模型。刚性模型适用于保持架刚度较大、变形可忽略的场景;柔性模型则更适用于塑料保持架等易发生弹性变形的结构,能更真实地反映碰撞过程中的能量吸收与动态响应。
两种模型均能输出丰富的动力学响应数据,为轴承设计、故障诊断与寿命预测提供了可靠的仿真工具。柔性保持架模型的引入,尤其适用于高速、冲击载荷等恶劣工况下的轴承性能评估。