# 行星齿轮内啮合副时变啮合刚度计算MATLAB程序套件详细介绍
## 一、程序概述
本程序套件基于**势能法**开发,专注于计算健康状态下行星齿轮内啮合副的**时变啮合刚度(TVMS)** ,核心针对“行星轮-内齿圈”啮合场景。程序严格遵循齿轮啮合力学原理,考虑了齿轮传动的关键几何与物理特性,同时适配行星轮系的运动特性,可用于齿轮动力学分析、振动噪声预测及故障诊断的基础刚度建模。
### 1.1 核心功能定位
– **计算对象**:行星齿轮系统中“行星轮(主动轮)-内齿圈(从动轮,固定)”的内啮合副。
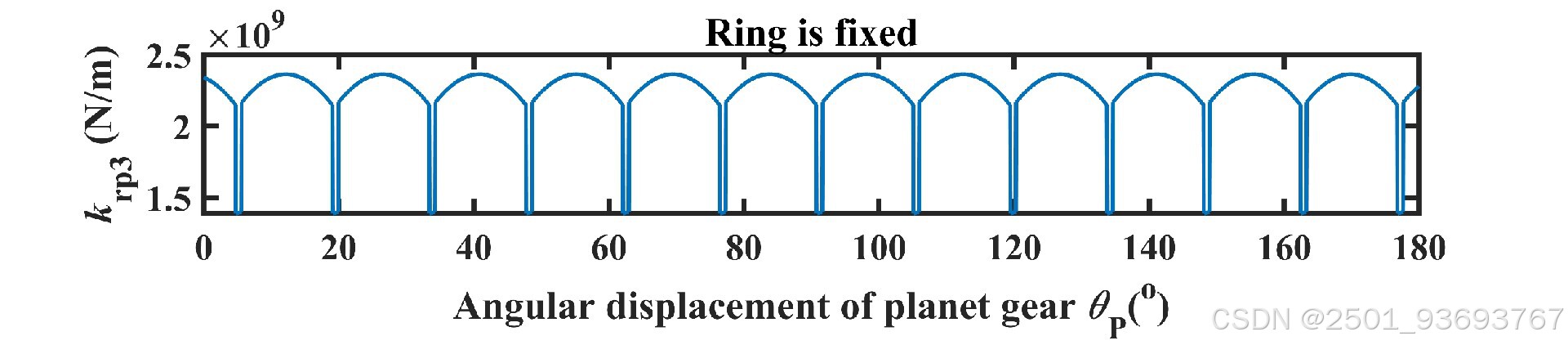
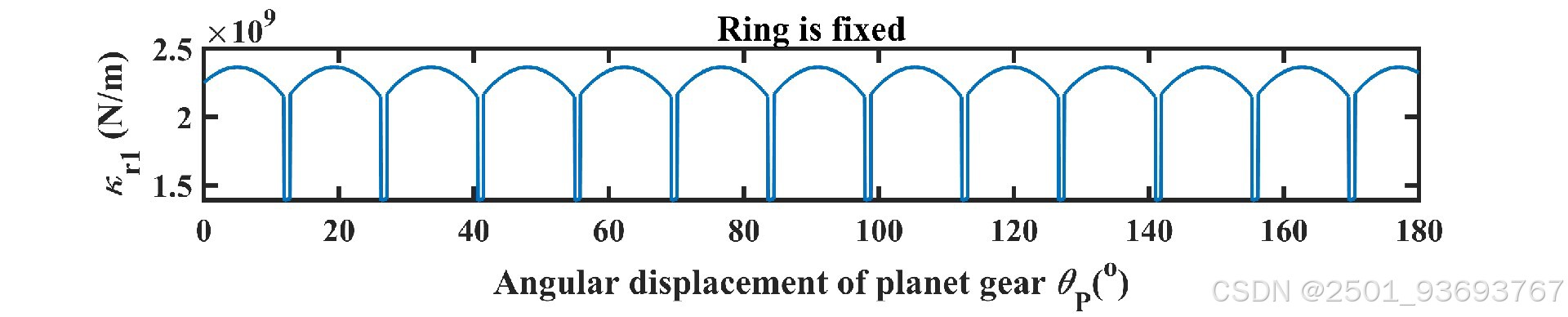
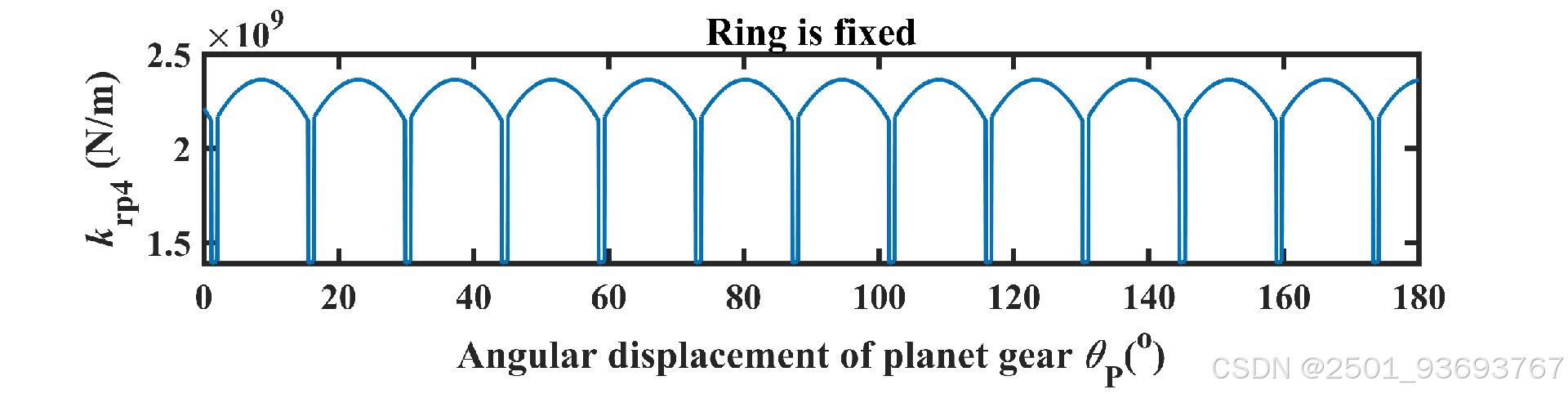
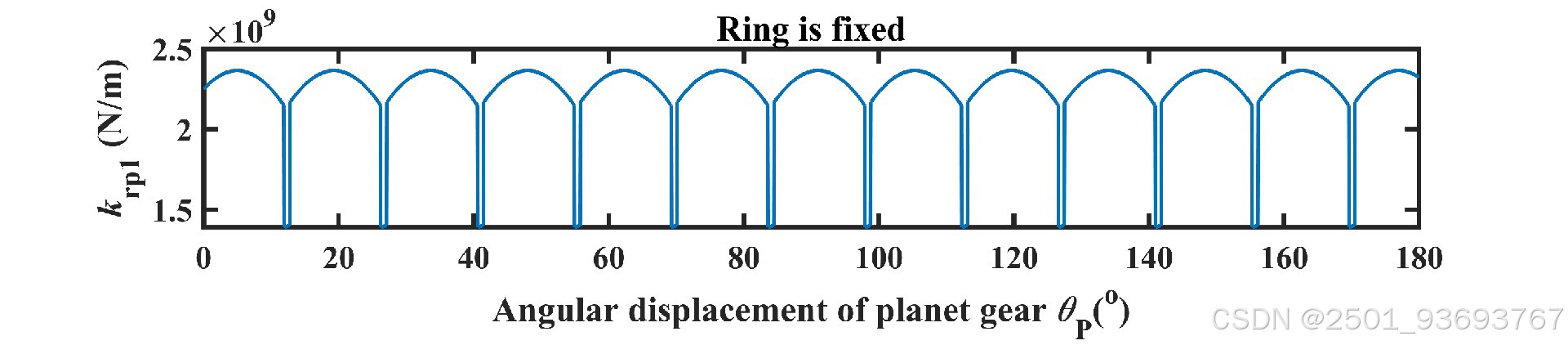
– **核心输出**:随行星架旋转角度变化的啮合刚度曲线(含单齿刚度、综合啮合刚度)。
– **适用场景**:健康齿轮的动力学建模、有限元(如ANSYS)结果验证、齿轮系统设计阶段的刚度特性分析。
### 1.2 程序文件构成
程序套件包含3个核心MATLAB脚本,功能各有侧重,可单独运行或配合使用,具体分工如下表所示:
| 文件名 | 核心功能 | 关键输出 | 适用场景 |
|—————-|——————————————|——————————————|——————————————|
| `inner_planetary_gear.m` | 计算内啮合副的**综合时变啮合刚度**,区分单齿/双齿啮合区 | 行星轮旋转角度-综合刚度曲线(含赫兹接触刚度) | 整体啮合刚度特性分析、系统动力学建模输入 |
| `single_tooth.m` | 拆分输出**单齿对刚度**(前齿对i、后齿对j),含主动轮/从动轮单独刚度 | 行星轮旋转角度-单齿对刚度曲线(主动轮/从动轮分别输出) | 单齿刚度验证、啮合区刚度贡献分析 |
| `single_tooth_R1.m` | 优化单齿刚度计算逻辑,聚焦**单个齿的独立刚度**(剔除冗余啮合对) | 行星轮旋转角度-单齿刚度曲线(行星轮/内齿圈明确标注) | 单齿刚度精准验证、有限元对比实验 |
## 二、关键理论基础与假设
### 2.1 核心计算方法:势能法
程序以**势能守恒原理**为核心,将齿轮啮合过程中的弹性变形能分解为4个部分,通过“总势能=各部分势能之和”推导刚度(刚度为势能对变形的二阶导数),具体分解如下:
– **弯曲变形能**:轮齿受载时产生的弯曲形变对应的能量,需考虑齿根过渡曲线与渐开线的连续几何特性。
– **剪切变形能**:轮齿剪切形变对应的能量,采用1.2修正系数(符合齿轮力学经典假设)。
– **压缩变形能**:轮齿接触区域压缩形变对应的能量,基于横截面面积与弹性模量计算。
– **赫兹接触变形能**:两齿面接触点的局部变形能量,采用赫兹接触理论公式计算接触刚度。
### 2.2 关键假设与边界条件
程序通过合理假设简化计算复杂度,同时保证工程精度,核心假设如下:
1. **内齿轮基体刚性**:不考虑内齿圈基体的弹性变形(因内齿轮基体刚度成熟计算公式缺失,且工程中内齿圈通常固定且刚度远大于轮齿)。
2. **运动约束**:内齿圈固定不动,行星架带动行星轮绕内齿圈旋转(符合行星轮系典型运动模式)。
3. **啮合相位差**:通过等分行星轮旋转角度、区分啮合周期内的齿对接触顺序,间接体现各啮合副的相位差异。
4. **健康齿假设**:不考虑轮齿裂纹、磨损、点蚀等故障,仅计算健康轮齿的啮合刚度。
## 三、程序核心特性与优势
### 3.1 精准的几何建模
1. **精确渐开线齿形**:通过渐开线方程(基圆、压力角、展角关联)计算齿面坐标,同时考虑**齿根过渡曲线**(基于齿条刀具加工原理,计算刀顶圆角对应的过渡曲线坐标),避免传统“简化齿形”带来的刚度计算误差。
2. **齿轮变位适配**:支持变位齿轮计算,通过输入变位系数(`xp`为行星轮变位系数,`xg`为内齿圈变位系数,由程序自动推导),适配非标准齿轮(如为避免根切、提高承载能力设计的变位齿轮)的刚度计算。
### 3.2 全面的物理特性考虑
程序在参数设置中涵盖齿轮传动的关键物理与几何参数,确保计算的工程实用性,核心参数如下表所示:
| 参数类别 | 参数符号 | 物理意义 | 示例值(程序默认) |
|—————-|———-|——————————————|————————–|
| 齿轮几何参数 | `Zs/Zp/Zr` | 太阳轮/行星轮/内齿圈齿数 | 21/33/87 |
| | `mn` | 法向模数 | 2.5mm(程序中单位为m) |
| | `alfa0` | 标准齿形角 | 20°(程序中转换为弧度) |
| | `hax/cx` | 齿顶高系数/顶隙系数 | 1.0/0.25 |
| 材料参数 | `E` | 弹性模量 | 2.068×10¹¹Pa(钢) |
| | `v` | 泊松比 | 0.3(钢) |
| | `G` | 剪切模量 | 由`E`和`v`自动推导(G=E/[2(1+v)]) |
| 运动参数 | `ns` | 太阳轮转速 | 1500r/min |
| | `Np` | 行星轮个数 | 4个 |
### 3.3 啮合过程精细化模拟
1. **啮合区划分**:自动区分“双齿啮合区”与“单齿啮合区”:
– 双齿啮合区:前齿对(即将退出啮合,标记为`i`)与后齿对(刚进入啮合,标记为`j`)同时接触,刚度为两齿对刚度叠加。
– 单齿啮合区:仅后齿对(`j`)接触,刚度为单齿对刚度。
2. **相位差体现**:通过`n_div=360*zp`(每转等分刻度数)将行星轮旋转一周划分为等角度步长,每个步长对应不同齿对的接触状态,间接体现多行星轮啮合时的相位差异。
## 四、程序结构与关键模块解析
### 4.1 通用程序框架(以`inner_planetary_gear.m`为例)
所有程序均遵循“参数初始化→几何/运动参数计算→刚度积分求解→结果绘图”的逻辑框架,核心模块分工明确,便于修改与扩展:
1. **模块1:参数初始化(齿轮基本参数)**
定义齿轮几何参数(齿数、模数、齿形角)、材料参数(弹性模量、泊松比)、运动参数(转速、行星轮个数),代码片段如下:
“`matlab
% 齿轮基本参数
hax=1.0; cx=0.25; % 齿顶高系数、顶隙系数
Zs=21; Zp=33; Zr=87; % 太阳轮/行星轮/内齿圈齿数
mn=2.5/1000; L=30/1000; % 模数(m)、齿宽(m)
alfa0=deg2rad(20); % 标准齿形角(rad)
E=2.068e11; v=0.3; G=E/(1+v)/2; % 弹性模量、泊松比、剪切模量
“`
2. **模块2:几何与运动参数计算**
基于齿轮啮合原理,自动推导分度圆半径、基圆半径、实际啮合角、变位系数、齿顶/根圆半径等关键参数,示例如下:
“`matlab
rp=mn*zp/2; rg=mn*zg/2; % 行星轮/内齿圈分度圆半径
alfa=acos(d0*cos(alfa0)/d); % 实际啮合角(考虑中心距变动)
rbp=rp*cos(alfa0); rbg=rg*cos(alfa0); % 基圆半径
rap=rp+(hax+xp+delty)*mn; rag=rg-(hax-xg+delty)*mn; % 齿顶圆半径
“`
3. **模块3:啮合起始/终止位置计算**
确定啮合起始点(`P1`)与分离点(`P2`)的坐标与角度参数,明确啮合长度与重合度(`CR`),代码逻辑如下:
“`matlab
PP1=rbg*(tan(alfa)-tan(alfaa_g)); % 节点P到起始点P1的距离
PP2=rbp*(tan(alfaa_p)-tan(alfa)); % 节点P到分离点P2的距离
P1P2=PP1+PP2; CR=P1P2/Pb; % 实际啮合长度、重合度
“`
4. **模块4:刚度积分求解(核心模块)**
通过**梯形数值积分法(`trapz`函数)** 计算轮齿的弯曲、剪切、压缩刚度(均为刚度的倒数积分,再求总刚度),同时叠加赫兹接触刚度,示例如下:
“`matlab
% 弯曲刚度积分(渐开线部分)
kbj2_p=trapz(tau,fkbj2_p); % 渐开线部分弯曲刚度倒数积分
kbj1_p=trapz(gamma,fkbj1_p); % 过渡曲线部分弯曲刚度倒数积分
kbjp=kbj1_p+kbj2_p; % 总弯曲刚度(倒数)
% 综合刚度计算(串联刚度叠加)
kt(m)=1./(1/kh+kbjp+ksjp+kajp+kbjg+ksjg+kajg); % 单齿啮合区总刚度
“`
5. **模块5:结果可视化**
绘制“行星轮旋转角度-刚度”曲线,标注坐标轴、图例,支持导出高清图(符合学术绘图规范),代码如下:
“`matlab
theta1=thetap/pi*180; % 角度转换(rad→°)
plot(theta1,kt*10^(-8),’LineWidth’,1.5); grid off;
xlabel(‘Rotation angle of planet gear \theta_P(°)’,’FontName’,’Times New Roman’);
ylabel(‘TVMS k_t (\times10^8 N/m)’,’FontName’,’Times New Roman’);
“`
### 4.2 `single_tooth_R1.m`的优化点
作为修改后的单齿刚度计算程序,`single_tooth_R1.m`在通用框架基础上做了以下优化,更适配单齿刚度验证场景:
1. **简化啮合对逻辑**:剔除“前齿对(i)”冗余计算,仅聚焦单个啮合对(j)的单齿刚度,避免多齿对干扰。
2. **明确刚度输出标注**:图例直接区分“行星轮单齿刚度(planet gear)”与“内齿圈单齿刚度(ring gear)”,且关闭图例边框(`set(h, ‘Box’, ‘off’)`),提升图面简洁度。
3. **调整啮合周期范围**:基于重合度(`CR`)确定啮合周期(`thetap=[0:2*pi/zp/1000:2*pi/zp*CR]`),确保覆盖完整啮合过程,无多余角度数据。
## 五、程序使用说明
### 5.1 环境要求
– **MATLAB版本**:兼容R2016b及以上版本(需支持`deg2rad`、`trapz`等基础函数)。
– **运行依赖**:无额外工具箱依赖,仅需MATLAB基础环境。
### 5.2 参数修改指南
用户可根据实际齿轮系统参数,在程序“参数初始化”模块修改以下关键参数(其余参数由程序自动推导,无需手动修改):
| 参数符号 | 修改说明 | 注意事项 |
|———-|——————————————|——————————————|
| `Zs/Zp/Zr` | 太阳轮/行星轮/内齿圈齿数 | 需满足行星轮系传动比关系(Zr=Zs+2*Zp,默认参数已满足) |
| `mn` | 法向模数(单位:m,默认2.5mm需转换为0.0025m) | 需与实际齿轮模数一致,单位转换需准确 |
| `L` | 齿宽(单位:m,默认30mm转换为0.03m) | 齿宽直接影响刚度大小,需准确输入 |
| `xp` | 行星轮变位系数(默认0,即标准齿轮) | 若为变位齿轮,需输入设计的变位系数 |
| `ns` | 太阳轮转速(单位:r/min,默认1500) | 影响啮合频率计算,需与实际工况一致 |
### 5.3 结果解读
程序运行后输出的核心结果为“旋转角度-刚度”曲线,需结合啮合区特性解读:
1. **双齿啮合区**:刚度值较高且相对平稳(两齿对刚度叠加),对应曲线的“平台段”。
2. **单齿啮合区**:刚度值较低且随角度变化(单齿对刚度,受齿面接触位置影响),对应曲线的“波动段”。
3. **单齿刚度验证**:`single_tooth_R1.m`输出的行星轮/内齿圈单齿刚度,可与有限元(如ANSYS)计算结果对比,验证势能法的准确性(程序作者提示:因假设与简化,结果可能存在小幅差异,需结合具体工况分析)。
## 六、程序局限性与注意事项
1. **内齿轮基体刚性假设**:程序未考虑内齿圈基体的弹性变形(因缺乏成熟计算公式),若需更精准结果,需结合有限元补充基体刚度修正。
2. **健康齿假设**:仅适用于无故障的健康齿轮,若需计算裂纹、磨损等故障状态的刚度,需扩展故障齿形建模模块。
3. **有限元对比提示**:程序作者明确说明“不保证与有限元结果完全吻合”,影响因素包括:基体刚度简化、赫兹接触假设、积分步长等,对比时需考虑这些简化带来的误差。
4. **相位差体现方式**:程序通过等分旋转角度间接体现相位差,未直接计算多行星轮的相位角,若需精准相位差分析,需在“运动参数计算”模块补充相位角公式。
## 七、参考文献与理论依据
程序开发严格参考齿轮力学与行星轮系领域的经典文献,确保理论正确性,核心参考文献如下:
1. Xihui Liang, Ming J. Zuo. *Analytically evaluating the influence of crack on the mesh stiffness of a planetary gear set* (2014)
2. 马辉, 左明键等. *Time-varying mesh stiffness calculation of cracked spur gears*(势能法计算时变啮合刚度的经典文献)
3. 罗阳, 马辉等. 行星齿轮系统动力学建模与刚度计算相关文献(程序备注中明确提及)
## 八、总结
本程序套件是行星齿轮内啮合副时变啮合刚度计算的高效工具,具有**几何建模精准、物理特性全面、使用便捷**的优势,可满足健康齿轮动力学分析的基础需求。`single_tooth_R1.m`作为优化后的单齿刚度计算程序,更适用于刚度验证与对比实验;`inner_planetary_gear.m`则适用于系统级动力学建模的综合刚度输入。
用户在使用时,需注意参数单位转换的准确性、实际工况与程序假设的匹配度,若需扩展至故障齿轮或更复杂场景,可基于现有框架补充故障建模、基体刚度修正等模块,进一步提升程序的工程适用性。